[Retourner à la galerie
d'images]
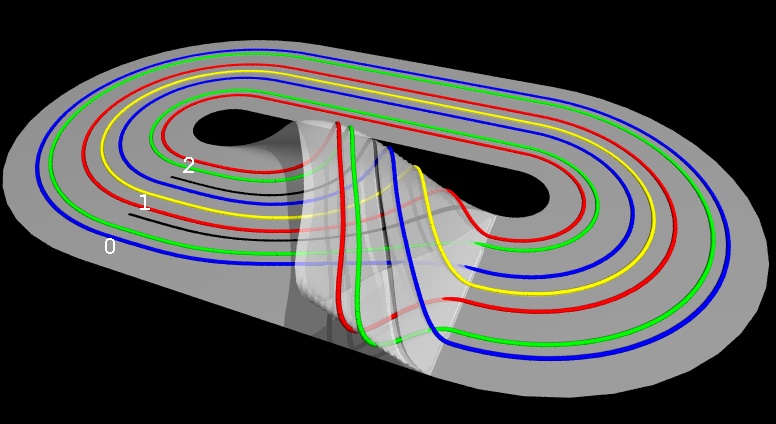
Organisation topologique d'un attracteur spirale M. Lefranc (PhLAM/CNRS)

Soumis le 5 Jan 2007 par Marc LEFRANC
Mot(s)-clé(s) : chaos, topologie, orbites périodiques instables
Cette surface bi-dimensionnelle à plusieurs branches (un gabarit, ou template en anglais) décrit de manière concise l'organisation topologique globale d'un attracteur "spirale", ou "entonnoir" ("funnel"), tel qu'on peut en observer dans le système de Rössler pour certaines valeurs des paramètres. En particulier, toutes les orbites périodiques instables de l'attracteur peuvent être projetées sur cette surface sans modifier leurs types de noeud ni leurs invariants topologiques. Sont ainsi représentées ici une orbite de période 1, en jaune, et trois orbites de période 2, en bleu, vert, rouge. Les quelques invariants décrivant la structure de cette surface fournissent des signatures des processus d'étirement et de repliement organisant la dynamique chaotique. La structure en branches fournit un codage symbolique naturel des orbites périodiques, énumérant les branches successivement visitées. Les codes des orbites représentées sont ainsi : 1 (jaune), 01 (bleu), 02 (vert), 12 (rouge). On voit sur cette figure que le code symbolique détermine les invariants topologiques de l'orbite. Inversement, les invariants d'une orbite permettent de remonter à son code symbolique.
IMAGES

Formation d'une circulation grande échelle (plus de détails...)
CONFÉRENCES
Auto-organisation en physique et en biologie, morphogenèse, ondes-particules, turbulence, physique non linéaire, Colloque International en mémoire d’Yves Couder à l'ENS et UPCité, 4 Juin 2024
Bifurcations and Instabilities in Fluid Dynamics, Edinburgh, Scotland, 24 Juin 2024
19e Journées de l'Hydrodynamique, Ecole Centrale de Nantes, 26 Novembre 2024